Absurdalne skojarzenia.
Nasz mózg działa w taki sposób, że łączy elementy na zasadzie skojarzeń. Być może absurdalne, ale proste i obrazowe, lepiej zapadają nam w pamięć.
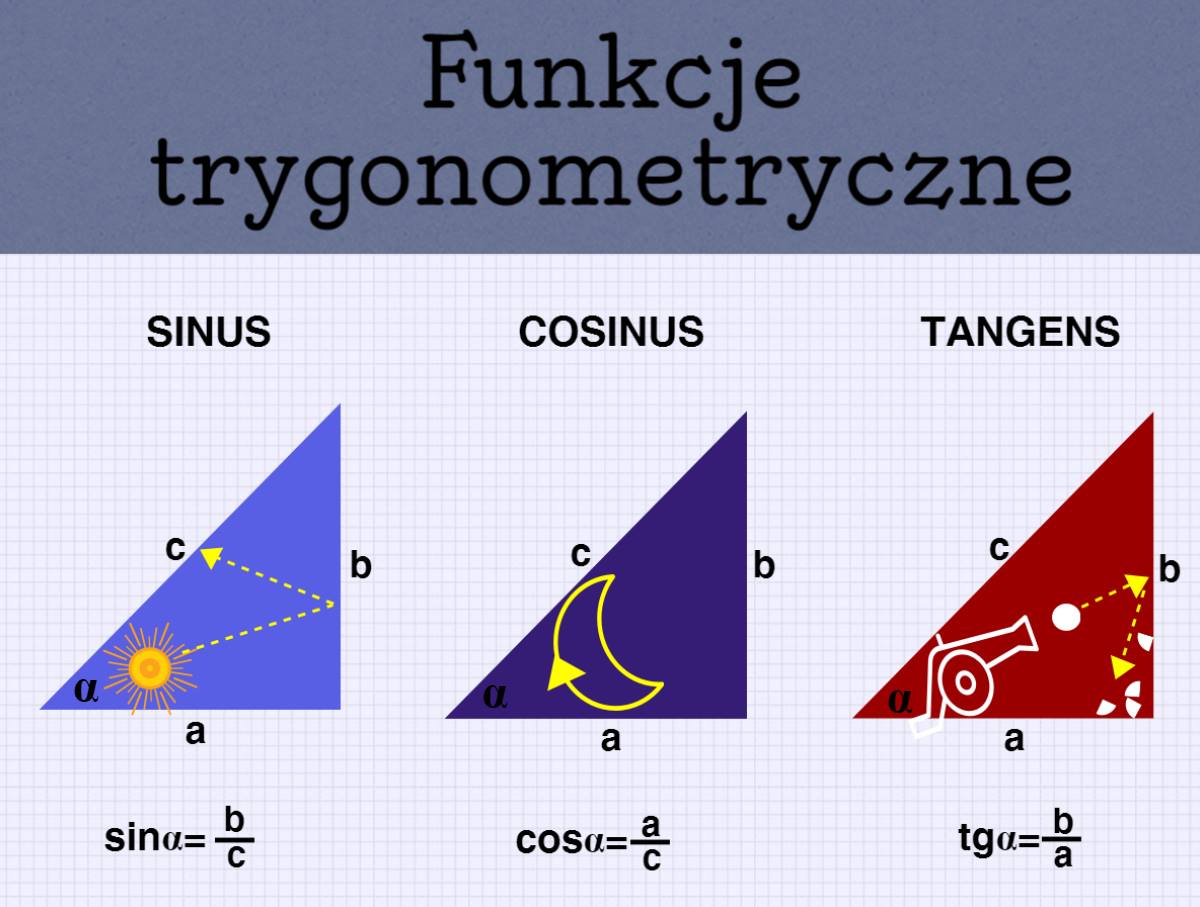
Poniżej przedstawiam Ci nietypowy, ale niezwykle skuteczny sposób na zapamiętanie wzorów funkcji trygonometrycznych. Moi uczniowie poznali już tę metodę, a nauczyciele, oddając poprawione sprawdziany, dziwią się na widok wszechobecnych słoneczek, księżyców i dział armatnich.
Okey. Ale jak połączyć nazwy funkcji trygonometrycznych ze słońcem, księżycem i armatą?
Nic prostszego:
sin - sun - z ang. Słońce
cos - c - litera 'c' przypomina kształtem księżyc ("rogalik" widoczny z Ziemi)
tg - tan - armata - ostatnie 2 litery słowa "armata" są jednocześnie pierwszymi dwiema w słowie "tangens".
Oczywiście możesz uczyć się też konwencjonalnymi metodami, np. zapamiętywać bezpośrednio z definicji:
"Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciw tego kąta do długości przeciwprostokątnej w tym trójkącie", ale... no właśnie.
Chyba sam dostrzegasz różnicę.
Inne przykłady niecodziennych metod, z którymi prawdopodobnie nie spotkałeś się w szkole:
1) cosinus "zjada" minus (jako jedyna funkcja trygonometryczna! Pozostałe go "wypluwają" :) - bardzo wymowny sposób na zapamiętanie parzystości i nieparzystości funkcji trygonometrycznych:
cos(-x) = cos(x) (cosinus zjada minus)
sin(-x) = -sin(x) (sinus go wypluwa)
tg(-x) = - tg(x) (tangens też go wypluwa)
ctg(-x) = - ctg(x) (cotangens też go wypluwa)
2) Metoda bystrego, ale płaczącego żółwia, czyli jak zapamiętać znaki funkcji trygonometrycznych.
Pewnie znany jest dla wielu wierszyk, który pozwala na zapamiętanie, w której ćwiartce, która funkcja trygonometryczna jest jakiego znaku. Na wszelki wypadek przytoczę: "w pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus".
Zauważyłem jednak, że wielu uczniów preferuje taką wersję:
ALL SMART TURTLES CRY
I ponownie, sentencja jest dosyć absurdalna, biorąc pod uwagę jej logiczne znaczenie "wszystkie bystre żółwie płaczą". No bo dlaczego te żółwie miałyby niby płakać?! I czy żółwie mogą w ogóle płakać? Natomiast ważna jest tu warstwa emocjonalna - dzieci uczą się szybciej, bo ich wyobraźnia od razu podsuwa im w głowie płaczące żółwie.
Wyjaśnienie metody:
Wierszyk mówi dokładnie o tym, w której ćwiartce, która funkcja przyjmuje wartości dodatnie:
- kolejne słowa oznaczają kolejne ćwiartki układu współrzędnych:
I. ALL - wszystkie - "w I wszystkie są dodatnie"
II. SMART - pierwsza litera S (sinus) - "w drugiej tylko sinus"
III. TURTLES - pierwsza litera T (tangens) - "w trzeciej tangens i cotangens"
IV. COSINUS - pierwsza litera C (cosinus) - "a w czwartej cosinus"
3) Wzory redukcyjne - ta metoda jest już znacznie częściej stosowana, lecz wciąż spotykam uczniów, którym nauczyciele w szkołach "każą" (a właściwie karzą, bo to wygląda na surową karę) uczyć się 16 wzorów, na które jest 1 prosta metoda.
Wyjaśnię na prostym przykładzie.
Chcemy obliczyć sin(240°)
KROK.1. Zapisujemy kąt 240° jako sumę lub różnicę kątów, z których jeden z kątów jest równy 90°,180°,270° lub 360° a drugi jest kątem ostrym. Np. 240° = 180°+60° albo 240° = 270°-30°.
KROK.2. Sprawdzamy czy dana funkcja jest dodatnia czy ujemna w danej ćwiartce (korzystając np. z "metody płaczących żółwii"): 240° to kąt z ćwiartki III, a sinus w III ćwiartce jest ujemny. Piszemy więc minus.
KROK.3. Jeśli w kroku 1 jako pierwszy składnik wybraliśmy 90° lub 270° wtedy funkcja przechodzi w kofunkcję (dla sinusa jest to cosinus, dla cotangensa tangens itd.), dla kątów 180°, 360° funkcja nie zmienia się.
KROK.4. Opuszczamy składnik 90°,180°,270° lub 360° wybrany w kroku I wraz ze znakiem stojącym przy kącie ostrym.
Podsumowując:
I. sposób: sin(240°)= sin(180°+60°) = -sin(60°)
II. sposób: sin(240°)= sin(270°-30°) = -cos(30°)
4) Wartości funkcji trygonometrycznych dla kątów 0°, 30°, 45°, 60°, 90°
- zamiast uczyć się na pamięć spójrz na poniższą infografikę





