
Trygonometria jest jednym z ważniejszych działów w matematyce. Na maturze nie obejdzie się bez zadań z wykorzystaniem funkcji trygonometrycznych. Jeżeli chcemy dobrze rozwiązywać zadania z trygonometrii, musimy zrozumieć zasadę ich działania, znać wzory, a także poprawnie korzystać z tablic trygonometrycznych. Dzisiaj przedstawimy Wam podstawowe pojęcia i zagadnienia, które musi znać każdy z Was.
Trygonometria - podstawy
Podstawy trygonometrii nie są bardzo skomplikowane. Zdecydowana większość zadań bazuje na wzorach, które w dużej mierze są dostępne w tablicach wzorów. Musimy jednak umieć korzystać z tablic trygonometrycznych. Nie musisz się martwić, że powinieneś znać te wartości na pamięć. Tablice z trygonometrii są dostępne na maturach i sprawdzianach z matematyki. Zacznijmy jednak od początku. Opowiemy Wam teraz o podstawach trygonometrii. Trygonometria określa nam zależności między bokami a kątami w trójkątach prostokątnych. Umiejętność wykorzystania wzorów i tablic pozwala nam na wyznaczenie wartości kątów, gdy znamy co najmniej dwie długości boków trójkąta lub, gdy znamy jeden kąt i jeden bok. Nie uda nam się jednak rozwiązać takich zadań bez tablic trygonometrycznych i wartości funkcji. Korzystanie z tablic nie jest trudne, jednak trzeba to zrozumieć. Jak raz się nauczysz, nie powinieneś mieć więcej problemów z odczytywaniem wartości.
Przydatne tablice z trygonometrii
Skoro już poznałeś podstawy trygonometrii czas pokazać Ci, jak wyglądają tablice trygonometrii oraz jak z nich korzystać. Tak jak wspominaliśmy, tablice są dostępne dla uczniów podczas sprawdzianów, czy nawet matury, więc nie musisz się uczyć tych wartości na pamięć. Musisz tylko odpowiednio odczytywać dane z tabeli. Poniżej przedstawiamy tabelę wartości zawartą w tablicy wzorów udostępnioną przez CKE dla maturzystów podczas pisania egzaminu - tej obowiązującej na maturze. W tablicach znajdziesz wartości kątów tj. sinusa, cosinusa i tangensa. Klucz do rozwiązywania zadań to prawidłowe odczytywanie wartości z tabelki. Jeżeli mamy zdanie, które będzie dotyczyło sinusa czy tangensa musimy skupić się na kolumnie po lewej stronie, jeżeli jednak zadanie dotyczy cosinusa, musisz przyjrzeć się wartościom umieszczonym w kolumnie po prawej stronie.
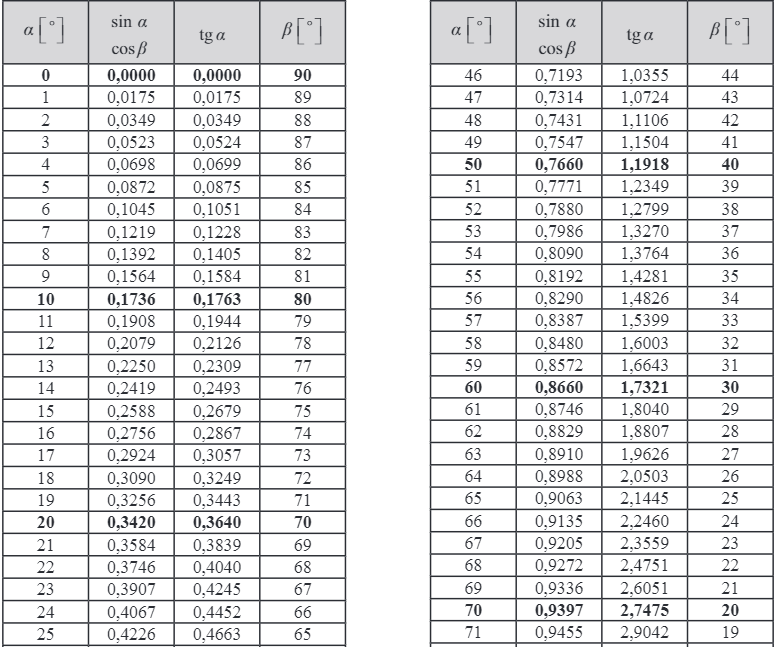
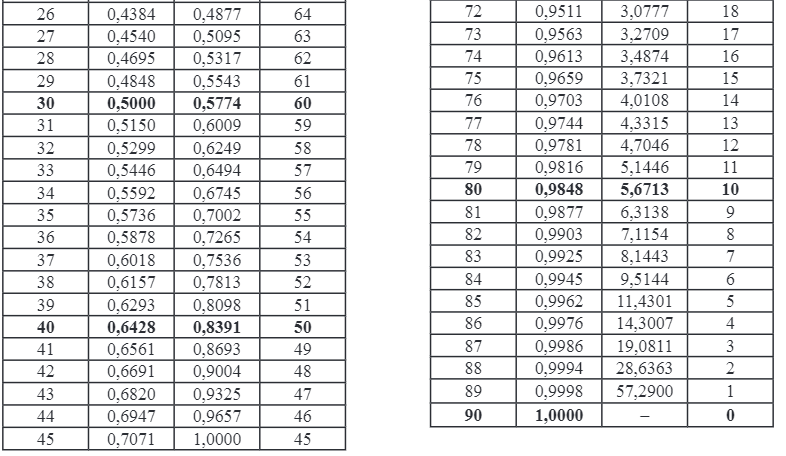
Wiemy, że początkowo wygląda to strasznie, ale zanim się zniechęcisz zobacz nasze dwa przykłady, jak korzystać z tablic trygonometrycznych.
- Przykład 1.
Podaj w przybliżeniu ile stopni ma kąt α, jeżeli sinus jest równu ⅗
W celu odpowiedzi na to pytanie musimy wykorzystać tablice trygonometryczne. Skoro wiemy, że sinus kąta α wynosi ⅗ . Musimy to przełożyć na ułamki dziesiętne. W takim wypadku otrzymujemy wartość 0,6. Teraz wystarczy znaleźć w wyżej umieszczonych tablicach wartość sinusa dla 0,6:

Nie ma idealnej wartości, dlatego szukamy tej najbardziej zbliżonej. W tym wypadku będzie to 0,6018. Oznacza to, że sinus ma taką wartość dla kąta 37°. I tyle. Nic więcej nie musimy robić. Odpowiedź można zapisać w taki sposób: α≈37°.
- Przykład 2.
Zastanówmy się teraz razem, jakie wartości przyjmuje sinus i tangens dla kąta 15°?
Wystarczy, że w lewej kolumnie znajdziemy wartość α=15°
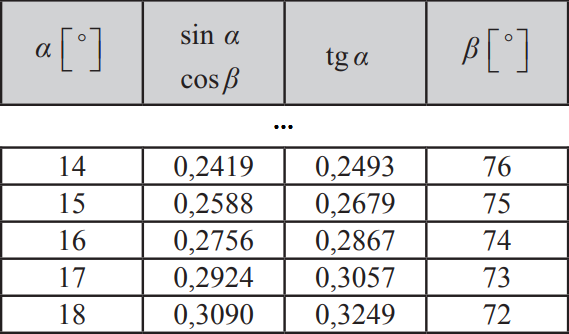
Z tabeli powyżej wynika, że sinα15° wynosi 02588 natomiast tgα15° = 0,2679
Tabele trygonometryczne przyjmują jeszcze inne wartości tj.:

Tablica przedstawiona powyżej służy do rozwiązywania zadań z trójkątami. Poniżej przykład:
- Przykład 3.
Podaj miarę kąta α

Przedstawione zadanie jest bardzo częste na maturze. Sprawdza umiejętność zapisywania i odczytywania funkcji trygonometrycznych. W pierwszej kolejności musimy obliczyć cosinusa.
Należy to zrobić ze wzoru, ponieważ znamy długości boków, które znajdują się przy α:

Następnie musimy odczytać wartość z wyżej przedstawionej tablicy trygonometrycznej. Z tabeli wynika, że cosα dla naszej wartości wynosi 30°.
Najczęściej spotykane wzory w trygonometrii
Trygonometria jest przepełniona wzorami. Na szczęście wiele z nich znajdziemy w tablicach matematycznych, które mogą nam towarzyszyć podczas sprawdzianów czy zadań z matematyki. Poniżej przedstawiamy wzory, które odnajdziesz w oficjalnej tablicy CKE.





Nie wszystkie wzory dotyczą podstawowej matury z matematyki. Wiele z nich jest przeznaczone dla osób, które będą zdawać maturę z matematyki na poziomie rozszerzonym. Na poziomie podstawowym przydadzą nam się jedynie wartości trygonometryczne (zarówno ta mała tabelka, jak i duża) oraz definicje funkcji trygonometrycznych w trójkątach prostokątnych, definicje funkcji trygonometrycznych oraz funkcje sumy i różnicy kątów.
Zadania z trygonometrii
Zadań z trygonometrii jest bardzo dużo. Nic dziwnego, nie znajdziemy chyba arkusza maturalnego, w którym nie byłoby chociaż jednego zadania z trygonometrii. Trygonometria jest działem matematyki, który wraca do nas także w innych zadaniach. Nie do końca związanych z trygonometrią, dlatego ważne jest dobre opanowanie tego materiału. W internecie znajdziemy bardzo dużo zadań dotyczących funkcji trygonometrycznych na przykład na stronach:
- http://www.matematykam.pl/
- https://www.matemaks.pl/
- https://www.matmana6.pl/
- https://zdajmyrazem.pl/
- https://szaloneliczby.pl/
Jak widzisz w internecie jest cała masa różnorodnych zadań. Wszyscy jednak wiemy, że samodzielne rozwiązywanie zadań nie zawsze wystarcza. Często musimy sięgnąć po pomoc kogoś bardziej doświadczonego. Korepetycje to dobry sposób zarówno dla osób, które nie rozumieją zagadnienia, jak i aspirują do zdawania matury na poziomie rozszerzonym. Wszystkie osoby, które są zainteresowane korepetycjami z matematyki zajęcia do zapoznania się z ofertą platformy BUKI. Nauczyciele zajmuje się udzielaniem lekcji zarówno stacjonarnie, jak i online. Zgodnie z Waszymi preferencjami.




